オイラーとゼータ関数

レオンハルト・オイラー　Leonhard Euler (1707-1783)

オイラーが計算したゼータ値

　「オイラーはどうしてゼータ値を26までしか求めなかったのか？」 ずっとそんな疑問を持っていました。しかし、実は34まで求められていたこと でほっと胸をなでおろすことができました。 詳しくいうと、オイラーは1734/35年の論文E41では6個の正の偶数での特殊値、 1745年の教本E101ではさらに7個（計13個）の特殊値、 1749年の論文E352ではさらに4個（計17個）の特殊値を示しています。 （論文E352は再び印刷されなかったため広く知られていなかった。）

　注目すべきなのは、ふたつの論文でのリストが2k=12、 34=37-3で終わっていることです。 非正則素数と指数の対(p,2k)の中で、 2kが最小となるのが(691,12)であり、 pが最小になるのが(37,32)です。 オイラーはそれらのことを認識した上で、計算していたと考えられるのです。 もし確実な証拠をご存知の方がおられましたら、 ぜひお教え下さい。(2004年6月-）
この考察の続き

題名が「美しい」理由

　ヒントはありました。 ゼータの正の値を月と書き、負の値を太陽と書いたことです。 太陽と月・・・とくれば日食（月食は地球の影響が必要なので不可） が思いつきます。 つまり、太陽（荒々しいゼータの負の値） を月（静かなゼータの正の値）が 隠そうとしますが、隠しきれなかった光の環 （巨大なガンマ関数の正の値）・（調和のとれた三角関数）／（不思議な円周率のべき乗） が輝くといったイメージです。 オイラーがきっとそう感じたように、 この数式の美しさをより強く明確に感じとることができました。 （下の図の左側が太陽のゼータ−右側が月のゼータの絶対値の対数値を表しています。 交代和なので極はありません。）

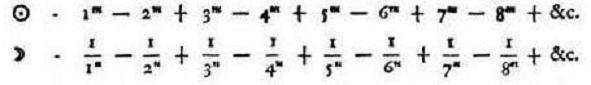
　もちろんオイラーが美しい日食を見ていないとすると、 この推測にもあまり説得力がありません。 日食に気が付いてネットで検索したところ、 論文E352を書く前年の1748年7月25日に日食を観測したという事実 (関連論文E117,E142)を知りました。 しかも、それはまさしく金環日食（Annular Eclipse）でした。

1748 Jul 25 11:27 A 122 0.518 0.946 48.7N 24.6E 59 231 05m12s
FIVE MILLENNIUM CATALOG OF SOLAR ECLIPSES 1701-1800
（Berlin 52.52N 13.40E）
下の写真は、日食に関する計算をおこなったオイラーに捧げられた地図 （Homann and Doppelmayr Astronomy Print）です。

次の画像で、オイラーの気持ちを想像することにしましょう。

オイラーはサンクト・ペテルブルグを1741年6月19日に出発し、ベルリンに1741年7月25日に到着した。（37日間）
ちょうど金環日食の7年前であった。
（2006年10月）

E41 -- De summis serierum reciprocarum (On the sums of series of reciprocals)
[written 1735, presented 1734, published 1740.] 論文１ 特殊値１

E72 -- Variae observationes circa series infinitas (Various observations about infinite series)
[written 1737, presented 1737, published 1744.] 論文２ オイラー積１ オイラー積２

E352 -- Remarques sur un beau rapport entre les series des puissances tant directes que reciproques (Remarks on a beautiful relationship between series of powers and reciprocals of powers)
[written 1749, presented 1761, published 1768.] 論文３ 特殊値３ 特殊値４ 関数等式１ 関数等式２ 関数等式３