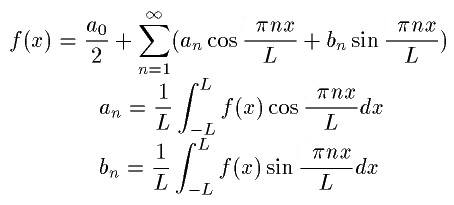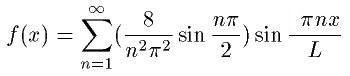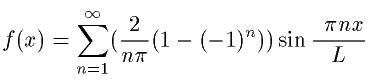音声と数学
 このページの目的
このページの目的
人間の感覚
音とは?
人工音声
人間の声
音声と関数
音声と線形空間
フーリエ級数
発展、未解決問題
フーリエ級数
さまざまな関数がこの世の中にはあります。その関数を三角関数の和として表そうというのがフーリエ級数です。三角関数はいろんな場面であらわれてくる特殊で重要な関数です。人間にはその特殊性を耳で感じる能力があるようで,三角関数の波形は「純」な音として聞こえます。そしてその「純」な関数を用いて複雑な関数を書き下そうというのです。
周期2Lの関数f(x)、すなわちどんなxに対してもf(x+2L)=f(x)となる関数を考えます。
すると、このf(x)は次のように書き下すことができます。(f(x)は区分的に連続であるとして積分ができるようにします。)
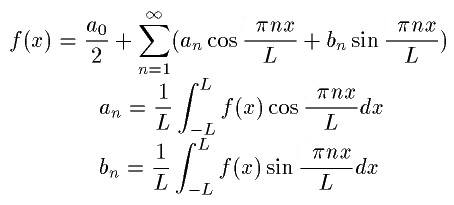
美しい式ですよね。そうじゃありませんか?実際に二つの関数をこのような形に書き下してみましょう。
三角波
周期0.05秒の三角波を考えてみましょう。
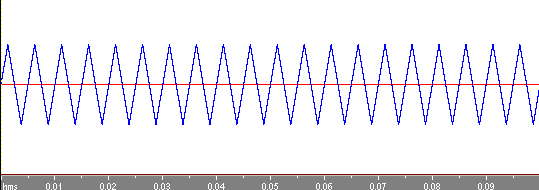
これを上の式に当てはめてみます。
奇関数なので、anは0になることが積分式から分かります。さらにbnを積分計算して求めてみるとf(x)は次のように書くことができます!
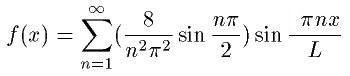
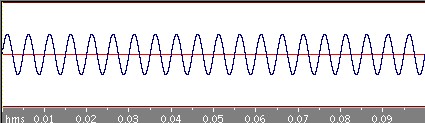
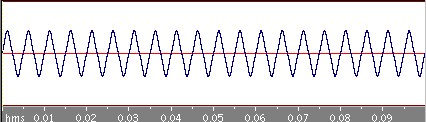
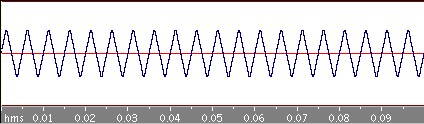
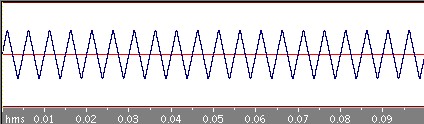
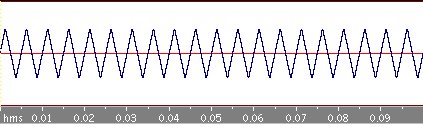
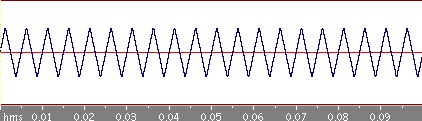
どんどん三角波に近づいていきますね。目と耳で確かめてください。
四角波
次は周期0.05秒の四角波です。
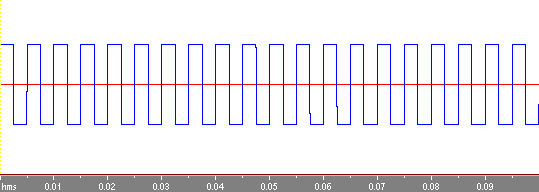
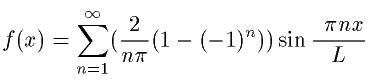
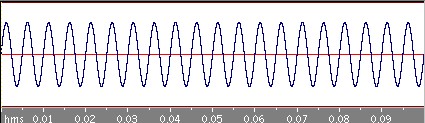
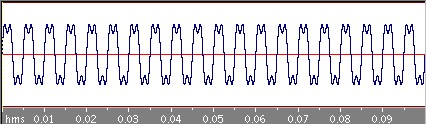
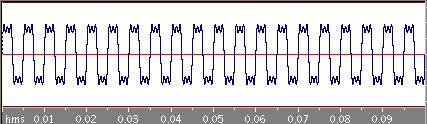
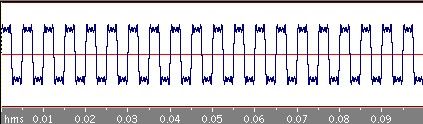
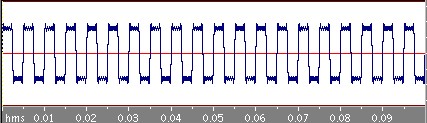
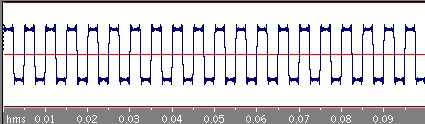
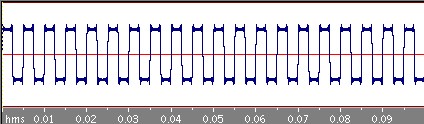
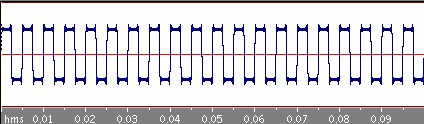
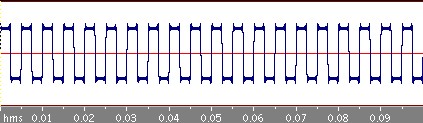
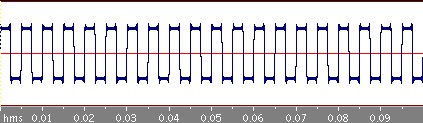
さきほどの三角波に比べるとなかなかもとの四角波に近づいていきませんね。三角波の場合はbnはnの二乗分の1に比例してどんどん減っていくのですが、この四角波の場合のbnはn分の1に比例しているのでそれほど減っていかないのです。
次に進む
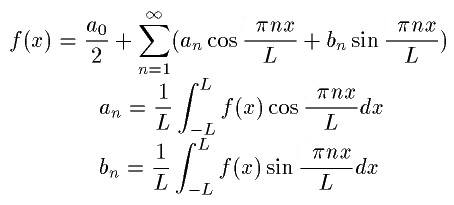
 このページの目的
このページの目的