音声と数学

音声と線形空間

線形代数というと行列式、連立一次方程式、逆行列、行列の対角化などのアルゴリズムを覚えてひたすら計算できるようになるというのが通例かもしれません。もちろんそれらができなければ相当にまずいことなのですが、ここでは線形空間というものの定義自体を考えてみることにします。

線形空間の定義を思い出します。はじめは頭が痛くなるといけないので、色文字以外は読み飛ばしてください。

Vが実数全体R上の線形空間であるとは次の性質を満たすことである。
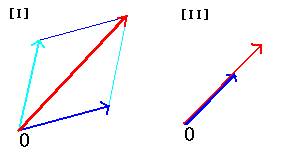
[I]　Vの任意の二元x,yに対して、加法x+yがVの中で定義される。
そして次の性質を満たす。(x,y,z∈V)
(1)　x+(y+z)=(x+y)+z　(分配法則）
(2)　x+0=0+x=x　（零元の存在）
(3)　x+(-x)=(-x)+x=0　（逆元の存在）
(4)　x+y=y+x　（可換性）
[II]　aを任意の実数、xをVの元に対して、スカラー乗法axが定義される。
そして次の性質を満たす。(a,b∈R,　x,y∈V)
(1)　(a+b)x=ax+bx　(分配法則）
(2)　a(x+y)=ax+by　(分配法則）
(3)　(ab)x=a(bx)　（結合法則）
(4)　1x=x　（単位元の存在）

難しい。。。そう思うのも無理はありません。最初からこんなにたくさんの性質を覚えられるものではないはずです。「どうしてもこの8つの性質を暗記しなければいけないの？」と尋ねたくなるでしょう。数学者に対してだったら、「そうだよ、体R上の加群のことをR上の線形空間というんだから、覚えなきゃねえ。」と答えるところです。でも相手が数学者以外なら「ううん、全部覚える必要はないよ。色文字だけ覚えてくれればいいよ。」と僕なら答えます。それなら、たったふたつだけです！すなわち、Vのなかでベクトルの足し算ができて、さらに実数をベクトルにかけることができれば、めでたくVはR上の線形空間というわけです。

あれっ？線形空間って、RとかR²とかR³とかじゃないの？そう、それは結局正しいことです。けれども、考え方によってはそれは間違っています。不思議な言い方ですが、その理由はこうです。あなたの線形空間に対するイメージは単に空間図形にとどまっているのではないでしょうか？それは最終的にはそうなってしまうのだけれど、本当はもっともっと複雑で面白い内容が詰まっているのです。音声、光、地震波、株価、気温、人口などの話はとても内容があって面白そうですが、結局それらは時間、位置などを変数とした関数と考えることができます。そして重要なことは、関数全体は自然に線形空間となるのです！すなわち前のページのように、加法を重ね合わせとし、スカラー乗法とは振幅の変化とすればいいのです。こうすれば、関数全体でなくても、連続関数全体、微分可能な関数全体などの部分集合もやはり線形空間になることがわかります。そしてこれらは、実数全体R上無限次元の空間になっているのです。「もし、株価の関数が分かったら」と考えれば、少しは興味が湧いてきませんか？ただ、これは私にとって相当に難しいことなので、今のところは音声の話で我慢してください。